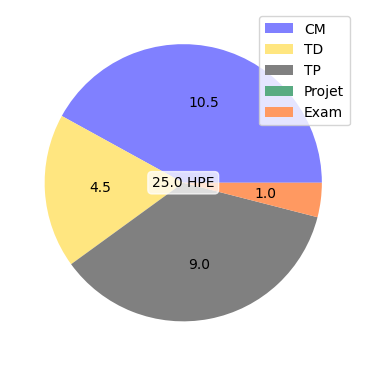
Optimisation

Optimization

Description: In this course, students are expected to acquire and master various fundamental aspects of continuous optimization. The following concepts will be covered and implemented in practice: formulation of optimization problems, conditions for the existence of global and local minimizers, convexity, duality, Lagrange multipliers, first-order methods, linear programming. The use of differentiable programming will be presented in practical work. Stochastic gradient-free methods, such as CMAES and PSO, will also be covered.

Learning outcomes: By the end of this course, students will master the fundamental concepts of continuous optimization (conditions for the existence of global and local minimizers, convexity, duality, Lagrange multipliers, first-order methods, linear programming, stochastic methods).

Evaluation methods: 1h written test, can be retaken

Evaluated skills:

• Physical Modeling
• Data Processing

Course supervisor: Michel Barret

Geode ID: SPM-MAT-004