Statistiques
Statistiques
Description : Dans ce cours, les étudiants devront acquérir les bases mathématiques, méthodologiques et numériques permettant de réaliser à partir d’observations d’un phénomène aléatoire (les données) une inférence sur la distribution de probabilité sous-jacente. Ainsi, ils seront en mesure d’analyser un phénomène passé ou de réaliser des prévisions pour un phénomène futur de nature similaire. Pour cela, les étudiants devront acquérir les formalismes, concepts et résultats élémentaires de la statistique mathématique. Cela inclut en particulier la définition de modèles statistiques, les principes de la théorie de l’estimation (estimateur du maximum de vraisemblance, estimateur bayésien, …) et de la théorie des tests d’hypothèses (test de Neyman-Pearson, test du khi-deux, test de Kolmogorov-Smirnov, …).
Acquis d’apprentissage : À l’issue de ce cours, les étudiants auront acquis un ensemble complet de connaissances mathématiques, méthodologiques et numériques essentielles pour effectuer des analyses statistiques approfondies à partir d’observations de phénomènes aléatoires (données). Ils seront en mesure de tirer des inférences sur la distribution de probabilité sous-jacente, ce qui leur permettra d’analyser des phénomènes passés et de formuler des prévisions pour des événements futurs de nature similaire. Les participants auront développé une compréhension approfondie des fondements de la statistique mathématique, y compris la création et la définition de modèles statistiques. Ils seront familiers avec les principes fondamentaux de la théorie de l’estimation, en utilisant des techniques telles que l’estimateur du maximum de vraisemblance et l’estimateur bayésien. De plus, ils seront compétents dans l’application des principes de la théorie des tests d’hypothèses, incluant des méthodes telles que le test de Neyman-Pearson, le test du khi-deux et le test de Kolmogorov-Smirnov. En résumé, ce cours dotera les étudiants des compétences nécessaires pour interpréter et analyser statistiquement des données, formuler des estimations fiables et mener des tests d’hypothèses rigoureux. Ces compétences seront cruciales pour prendre des décisions éclairées basées sur des observations empiriques et pour contribuer de manière significative à la résolution de problèmes dans divers domaines.
Modalités d’évaluation : Examen écrit de 1h30, rattrapable.
Compétences évaluées :
- Traitement Données
Responsable de cours :
- Joël Legrand
Identifiant Geode : SPM-MAT-003
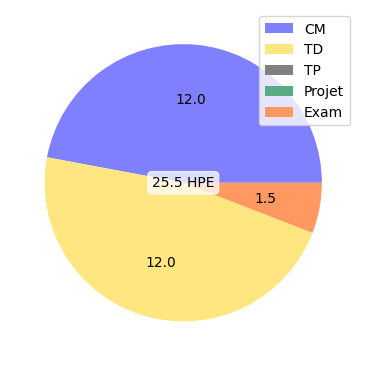
CM :
- Introdution et méthodes d’estimation ponctuelle (1.5 h)
- Comparaison d’estimateurs et propriétés asymptotiques (1.5 h)
- Intervale de confiance (1.5 h)
- Estimation bayésienne (1.5 h)
- Tests d’hypothèses (1.5 h)
- Tests ANOVA (1.5 h)
- Régression linéaire (1.5 h)
- Régression logistique, GLM (1.5 h)
TD :
- Introdution et méthodes d’estimation ponctuelle (1.5 h)
- Comparaison d’estimateurs et propriétés asymptotiques (1.5 h)
- Intervale de confiance (1.5 h)
- Estimation bayésienne (1.5 h)
- Tests d’hypothèses (1.5 h)
- Tests ANOVA (1.5 h)
TP :
- Régression linéaire (1.5 h)
- Régression logistique, GLM (1.5 h)