Statistiques

Statistics

Description: In this course, students will acquire the mathematical, methodological, and computational foundations necessary to perform inference on the underlying probability distribution from observations of a random phenomenon (the data). This will enable them to analyze past phenomena or make forecasts for future events of a similar nature. To achieve this, students will learn the basic formalisms, concepts, and results of mathematical statistics. This includes, in particular, the definition of statistical models, the principles of estimation theory (maximum likelihood estimator, Bayesian estimator, etc.), and hypothesis testing theory (Neyman-Pearson test, chi-squared test, Kolmogorov-Smirnov test, etc.).

Learning outcomes: By the end of this course, students will have acquired a comprehensive set of mathematical, methodological, and computational skills essential for conducting in-depth statistical analyses based on observations of random phenomena (data). They will be able to draw inferences about the underlying probability distribution, enabling them to analyze past events and make forecasts about future events of a similar nature. Participants will have developed a solid understanding of the foundations of mathematical statistics, including the creation and definition of statistical models. They will be familiar with the core principles of estimation theory, using techniques such as the maximum likelihood estimator and the Bayesian estimator. In addition, they will be proficient in applying the principles of hypothesis testing theory, including methods such as the Neyman-Pearson test, the chi-squared test, and the Kolmogorov-Smirnov test. In summary, this course will equip students with the necessary skills to interpret and statistically analyze data, formulate reliable estimates, and carry out rigorous hypothesis tests. These competencies will be essential for making informed decisions based on empirical observations and for contributing meaningfully to problem-solving across a wide range of fields.

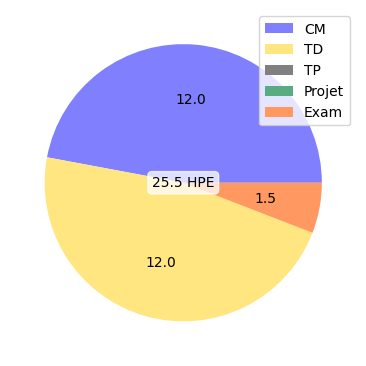
Evaluation methods: 1h30 written test, can be retaken.

Evaluated skills:

• Data Processing

Course supervisor:

• Michel Barret
• Joël Legrand

Geode ID: SPM-MAT-003