Probabilités

Description : À l’issue du cours de probabilité du tronc commun, les élèves maîtriseront les concepts d’expérience aléatoire, d’espace probabilisé, de loi de probabilité, de variables aléatoires (VA), de conditionnement et d’indépendance de VA. Ils sauront construire un espace probabilisé adapté à une expérience aléatoire (et inversement), calculer et utiliser les moments de VA réelles ou complexes, reconnaître et utiliser la structure d’espace de Hilbert des VA complexes du second ordre, identifier et utiliser les différentes représentations de lois de probabilité (fonction de répartition, densité de probabilité, fonctions caractéristiques, …), identifier des modèles de lois de probabilité (Bernoulli, binomiale, Poisson, gaussienne, etc.), reconnaître et utiliser les différents types de convergence de suites de VA. Enfin, ils sauront justifier et appliquer les théorèmes fondamentaux de la théorie des probabilités (théorème central limite, loi des grands nombres, etc.), reconnaître et utiliser le concept d’espérance conditionnelle.

Acquis d’apprentissage : À l’issue de ce cours, les élèves sauront: utiliser les concepts d’expérience aléatoire, d’espace probabilisé, de loi de probabilité, de variables aléatoires (VA), de conditionnement et d’indépendance de VA; construire un espace probabilisé adapté à une expérience aléatoire et inversement; calculer et utiliser les moments de VA réelles ou complexes; reconnaître et utiliser la structure d’espace de Hilbert des VA complexes du second ordre; identifier et utiliser les différentes représentations de lois de probabilité (fonction de répartition, densité de probabilité, fonctions caractéristiques, …) ; identifier des modèles de lois de probabilité (Bernoulli, binomiale, Poisson, gaussienne, etc.) ; reconnaître et utiliser les différents types de convergence de suites de VA ; justifier et appliquer les théorèmes fondamentaux de la théorie des probabilités (théorème central limite, loi des grands nombres, etc.) ; reconnaître et utiliser le concept d’espérance conditionnelle.

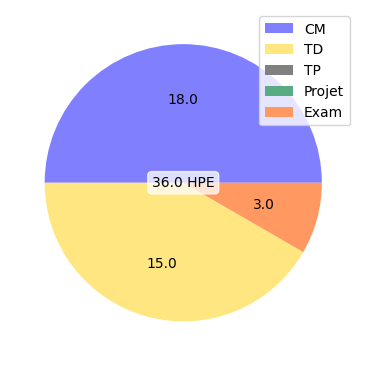
Modalités d’évaluation : Examen écrit de 1h30, rattrapable.

Responsable de cours : Michel Barret

Identifiant Geode : SPM-MAT-002

CM :

Introdution aux espaces probabilisés 1/2 (1.5 h)
Introdution aux espaces probabilisés 2/2 (1.5 h)
Moments des variables aléatoires 1/2 (1.5 h)
Moments des variables aléatoires 2/2 (1.5 h)
Fonctions caractéristiques et suites de VA indépendantes 1/2 (1.5 h)
Fonctions caractéristiques et suites de VA indépendantes 2/2 (1.5 h)
Loi et espérance conditionnelle 1/2 (1.5 h)
Loi et espérance conditionnelle 2/2 (1.5 h)

TD :

Introdution aux espaces probabilisés (1.5 h)
Moments des variables aléatoires 1/2 (1.5 h)
Moments des variables aléatoires 2/2 (1.5 h)
Fonctions caractéristiques et suites de VA indépendantes 1/2 (1.5 h)
Fonctions caractéristiques et suites de VA indépendantes 2/2 (1.5 h)
Loi et espérance conditionnelle 1/2 (1.5 h)
Loi et espérance conditionnelle 2/2 (1.5 h)