Optimisation
Optimisation
Description : Dans ce cours les élèves devront acquérir et maîtriser divers aspects fondamentaux de l’optimisation continue. Les notions suivantes seront abordées et mises en oeuvre pratiquement: formulation des problèmes d’optimisation, conditions d’existence de minimiseurs globaux et locaux, convexité, dualité, multiplicateurs de Lagrange, méthodes du premier ordre, programmation linéaire. L’utilisation de la programmation différentiable sera présentée en travaux pratiques. Les méthodes stochastiques ‘gradient-free’, comme CMAES et PSO, seront également abordées.
Acquis d’apprentissage : À l’issue de ce cours, les élèves maîtriseront les concepts fondamentaux de l’optimisation continue (conditions d’existence de minimiseurs globaux et locaux, convexité, dualité, multiplicateurs de Lagrange, méthodes du premier ordre, programmation linéaire, méthodes stochastiques).
Modalités d’évaluation : Examen écrit 1h, rattrapable
Compétences évaluées :
- Modélisation Physique
- Traitement Données
Responsable de cours : Michel Barret
Identifiant Geode : SPM-MAT-004
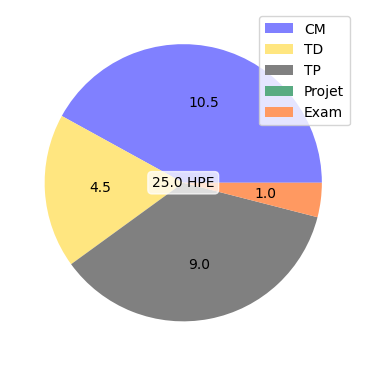
CM :
- Bases de l’optimisation (3.0 h)
- Convexité, quelques algorithmes itératifs (1.5 h)
- Dualité (1.5 h)
- Programmation linéaire (1.5 h)
- Méthode des multiplicateurs de Lagrange (1.5 h)
- Méthodes stochastiques gradient-free (1.5 h)
TD :
- Dualité (1.5 h)
- Méthode des multiplicateurs de Lagrange (1.5 h)
- Programmation linéaire (1.5 h)
TP :
- Bases de l’optimisation (3.0 h)
- Convexité, quelques algorithmes itératifs (3.0 h)
- Méthodes stochastiques gradient-free (3.0 h)