Systèmes Complexes
Physique des Systèmes Complexes
Description : La physique des systèmes complexes explore les comportements émergents et les propriétés collectives résultant de l’interaction entre un grand nombre de systèmes dynamiques, d’agents, ou de composants. Ce cours offre une introduction approfondie à cette discipline, en mettant l’accent sur les la théorie et la dynamique, les phénomènes émergents, les notions de synchronisation et les phénomènes épidémkques sur les réseaux.
Bibliographie :
- Ref. [1] : A.-L. Barabasi, Network Science, Cambridge University Press (2016)
- Ref. [2] : P. Fieguth, An Introduction to Complex Systems, Springer, 2nd Ed. (2020)
Acquis d’apprentissage : A l’issue de cours, les étudiants pourront : AA1 : Définir, expliquer et identifier les cas d’application des principaux concepts de la physiques des systèmes complexes – AA2 : Analyser des phénomènes critiques tels que les transitions de phases – AA3 : Modéliser et analyser des systèmes en interaction dans différents domaines en utilisation la physique des réseaux et la simulation numérique – AA4 : Modéliser, analyser et simuler des phénomènes de synchronisation ou des phénomènes épidémiques – AA5 : Exploiter les dynamiques collectives pour le calcul analogique et l’apprentissage machine physique
Modalités d’évaluation : Mini projet
Compétences évaluées :
- Modélisation Physique
- Traitement Données
Responsable de cours :
- Damien Rontani
Identifiant Geode : SPM-PHY-008
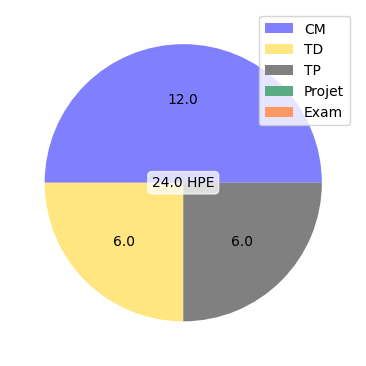
CM :
- Introduction à la théorie des réseaux (3.0 h)
- Dynamiques sur les réseaux (1.5 h)
- Phénomènes émergents (3.0 h)
- Synchronisation (3.0 h)
- Information et entropie (1.5 h)
TD :
- Introduction à la théorie des réseaux (1.5 h)
- Dynamiques sur les réseaux (1.5 h)
- Phénomènes émergents (1.5 h)
- Synchronisation (1.5 h)
TP :
- Travaux Expérimentaux (TrEx)1/2 (3.0 h)
- Travaux Expérimentaux (TrEx)2/2 (3.0 h)